Chapter 5.4 Instruction-Level Parallelism

本节我们会基于一个合并运算的代码，使用不同的方法对其进行一系列的优化，并使用每元素的周期数（Cycles Per Element, CPE）作为表示程序性能的度量标准。

该代码使用某种运算，将一个向量中所有的元素合并为一个值，其初始实现如下：

void combine1(vec_ptr v, data_t *dest)
{
    long i;
    *dest = IDENT;
    for (i = 0; i < vec_length(v); i++) 
    {
        data_t val;
        get_vec_element(v, i, &val);
        *dest = *dest OP val;
    }
}

其中常数IDENT和操作OP由编译时的不同定义来决定：

  • #define IDENT 0和#define OP +表示对向量元素求和。

  • #define IDENT 1和#define OP *表示计算向量元素的乘积。

通过进行我们前面介绍的最基础的机器无关优化，包括编译器自行优化，消除循环的低效率（代码移动）和减少内存引用，我们可以很轻松地将代码优化为下面这个版本：

void combine4(vec_ptr v, data_t *dest)
{
  long i;
  long length = vec_length(v);
  data_t *d = get_vec_start(v);
  data_t acc = IDENT;
  for (i = 0; i < length; i++)
      acc = acc OP d[i];
  *dest = acc;
}

程序性能的变化如下：

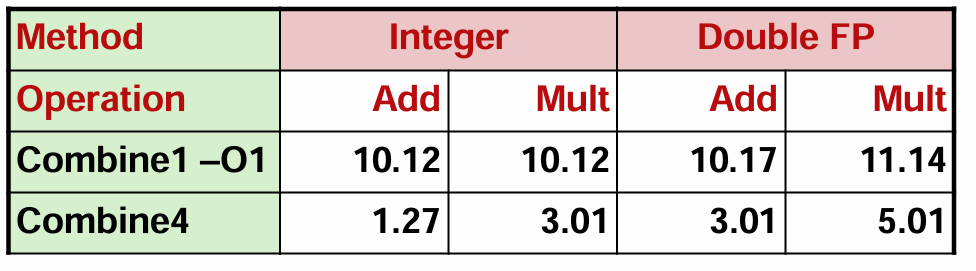
Effect of Basic Optimizations

事实上，经过基础优化的代码已经接近延迟界限，参考上一节我们介绍的参考机各操作的延迟：

Integer AddInteger MultiplySingle/Double FP AddSingle/Double FP Multiply
1335

对比之下，细心的你可能会产生一个疑问：为什么整数乘法（3.01 vs 3）、浮点数加法（3.01 vs 3）和乘法（5.01 vs 5）都逼近延迟界限，但整数加法（1.27 vs 1）似乎还留有余地呢？这和循环开销有关，一般来说，循环次数越多，开销越大。由于整数乘法和浮点数运算循环本身开销较大，循环带来的额外开销对它们影响并不明显；但由于整数加法本身开销小，所以循环的额外开销就会显著地影响到整数加法的性能。因此我们采用循环展开的方法进行优化。

Loop Unrolling

循环展开是一种程序变换，通过增加每次迭代计算的元素的数量，减少循环的迭代次数。

针对前例，我们可以使用2x1循环展开，即每次循环处理两个元素。

void combine5(vec_ptr v, data_t *dest)
{
    long length = vec_length(v);
    long limit = length-1;
    data_t *d = get_vec_start(v);
    data_t acc = IDENT;
    long i;
    /* Combine 2 elements at a time */
    for (i = 0; i < limit; i+=2) 
    {
        acc = (acc OP d[i]) OP d[i+1];
    }
    /* Finish any remaining elements */
    for (; i < length; i++) 
    {
        acc = acc OP d[i];
    }
    *dest = acc;
}

让我们再看一看程序性能：

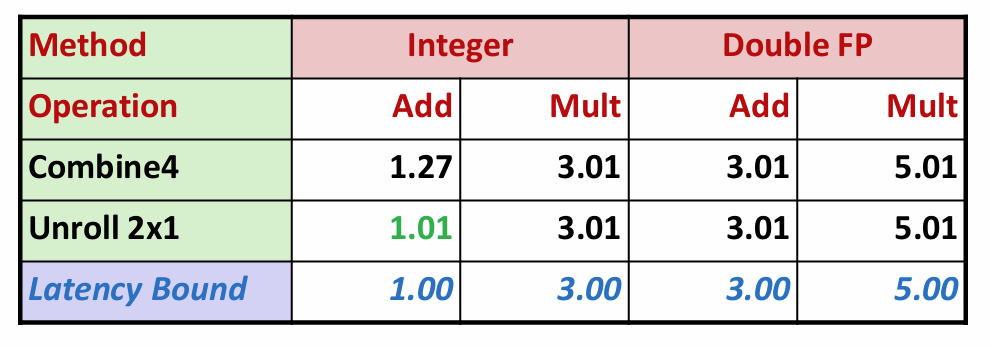
Loop Unrolling

现在所有的操作都达到了延迟界限！

但是这还不够，我们的目标是突破延迟界限，达到吞吐量界限。循环展开无法突破延迟界限的原因是，在每次迭代中存在必须顺序执行的两个乘法。因此要想突破此界限，必须要突破顺序相关，提高并行性。

Reassociation Transformation

重新结合变换是一种打破顺序相关从而使性能提高到延迟界限之外的方法。

在本例中，我们仅将combine5中的语句acc = (acc OP d[i]) OP d[i+1];修改为acc = acc OP (d[i] OP d[i+1]);。即改变了括号的位置，如下：

void combine6(vec_ptr v, data_t *dest)
{
    long length = vec_length(v);
    long limit = length-1;
    data_t *d = get_vec_start(v);
    data_t acc = IDENT;
    long i;
    /* Combine 2 elements at a time */
    for (i = 0; i < limit; i+=2) 
        acc = acc OP (d[i] OP d[i+1]);
    /* Finish any remaining elements */
    for (; i < length; i++)
        acc = acc OP d[i];
    *dest = acc;
}

你可能想问，只是括号的位置变了一下，这能有什么影响？但是当我们测量CPE时，得到令人吃惊的结果：

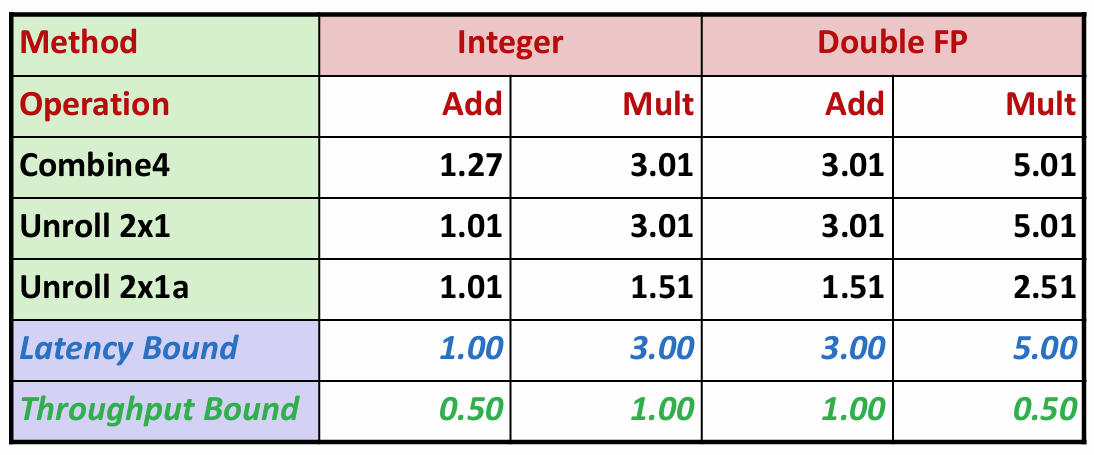
Reassociation Transformation

采用2x1a展开的combine6中，整数加的性能和采用2x1展开的combine5性能相同，而其他三种情况达到了2x1展开的两倍，突破了延迟界限！

下图说明了产生该巨大影响的原因：

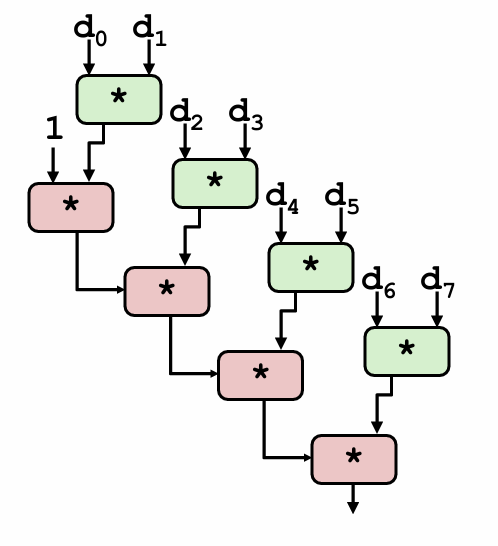
Reassociation Transformation

括号位置变化后，下一次迭代中(d[i] OP d[i+1])可以提前进行，不需要等待前一次迭代的累积值，即突破了顺序相关性。因此，最小可能的CPE减少为原来的一半。

可以看到，重新结合变换能够减少计算中关键路径上操作的数量，通过更好地利用功能单元的流水线能力得到更好的性能。

Multiple Accumulators

另一种方式是引入多个累积变量。由于执行加法和乘法的功能单元是完全流水线化的，理论上它们可以每个时钟周期开始一个新操作。但是在combine5中，由于我们将累积值放在一个单独的变量acc中，在前面的计算完成之前，都无法计算acc的新值。虽然计算acc新值的功能单元能够每个时钟周期开始一个新的操作，但是由于这种顺序依赖，它只能每L个周期开始一条新操作（L是合并操作的延迟）。

在本例中，我们引入两个累积变量来打破这种顺序相关，将一组合并运算分割成两个部分，并在最后合并结果，并称之为2x2展开。

void combine7(vec_ptrv,data_t*dest)
{
  long i;
  long length=vec_length(v);
  long limit=length-1;
  data_t* data=get_vec_start(v);
  data_t acc0=IDENT;
  data_t acc1=IDENT;
 
  /*Combine 2 elements at a time*/
  for(i=0;i<limit;i+=2)
  {
     acc0=acc0 OP data[i];
     acc1=acc1 OP data[i+1];
  }
 
  /*Finish any remaining elements*/
  for(;i<length;i++)
     acc0=acc0 OP data[i];
  *dest=acc0 OP acc1;
}

采用2x2展开的combine7版本的实际运行过程如下：

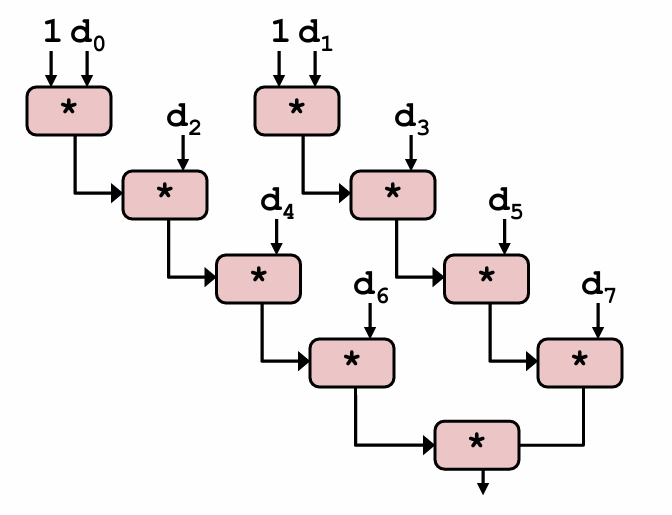
Multiple Accumulators

我们引入的两个累积变量使它能够同时利用两个加载功能单元，处理器不再需要延迟一个加法或乘法操作以等待前一个操作完成。这实际上形成了两条独立的操作流，一条处理偶数索引的计算，一条处理奇数索引的计算。

我们的程序性能也因此得到了更进一步的提升：

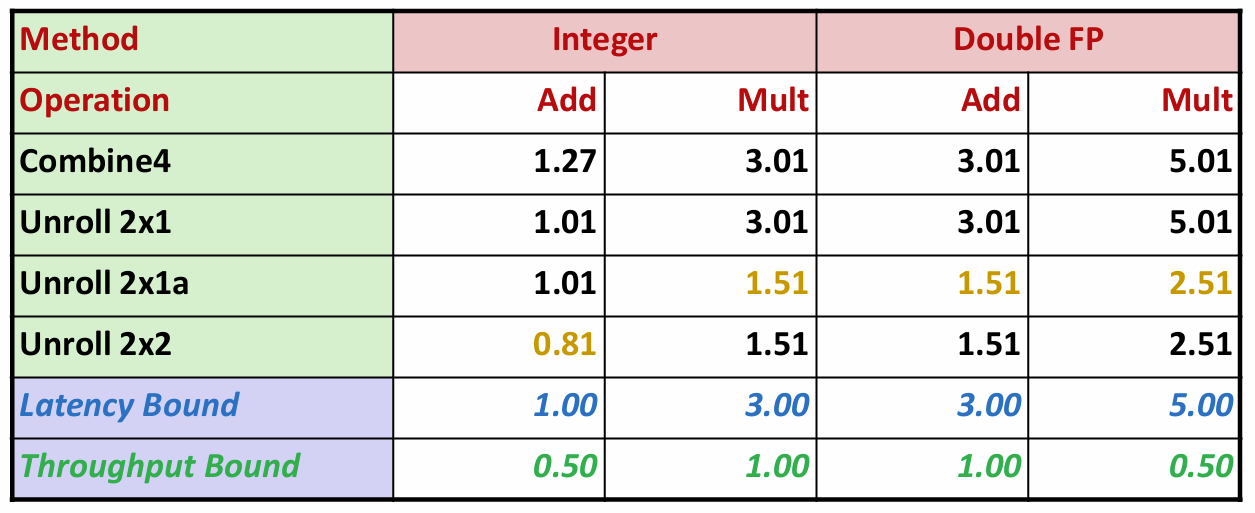
Multiple Accumulators

这一次，除了整数乘、浮点数加乘和2x1a展开的combine6版本性能相同外，整数加法性能又得到了提升。

重复实验结果表明，采用上述两种方法，我们的合并函数最终能达到下面的性能：

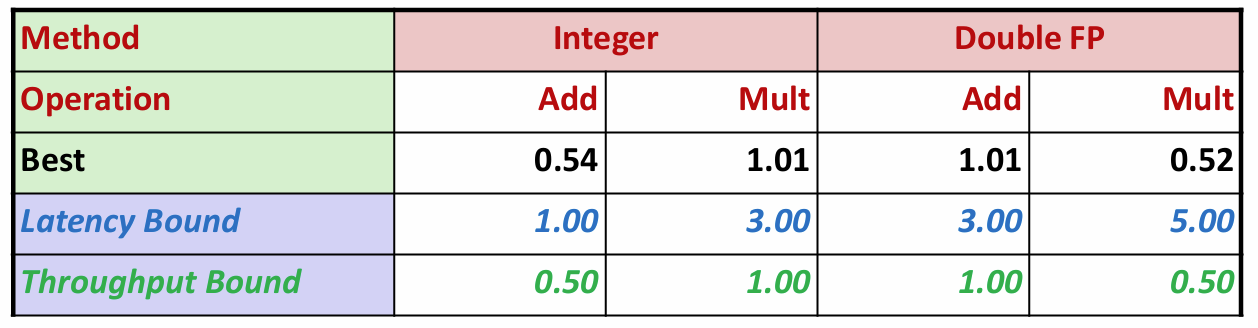
Combine function

即使用以上优化技术，程序的CPE已经接近于吞吐量界限。

© 2025. ICS Team. All rights reserved.