XJTU-ICS Lab 5: Optimization Lab¶

实验简介¶

课堂上老师介绍了许多程序优化技巧，相同的算法稍作变换，借助编译器的帮助，运行效率就可以成倍甚至成十倍地提升，不知道有没有给到同学们一点小小的系统震撼。看到这些魔术一般的优化，同学们有没有跃跃欲试，想要在真实系统中优化一段代码，并测量其性能呢？

本次实验我们来优化一段计算多项式值的代码，并且亲自测量其性能，希望能加深同学们对机器特定优化的理解，同时为同学们提供测量性能的经验。

实验环境准备¶

本次实验使用一台新的 ARM 服务器。由于实验结果与 CPU 型号强相关，本次试验只能远程进行。连接方式、账户名称等与以前的实验相同，但是服务器域名变成了 arm.ics.xjtu-ants.net，端口号为 22。具体的操作请参考原来的环境配置说明。

我们强制你在首次登陆时修改你的初始密码，vscode 可能不支持这一操作，请使用命令行 ssh 登陆后进行修改（Powershell/cmd on Windows, bash on Linux/Mac OS），再尝试 vscode 登陆即可。

注意事项¶

本次实验的机器使用鲲鹏 920 CPU，是一个 ARM 体系结构的 CPU，与课本上介绍的 x86-64 体系结构共享许多概念。课上的论述都可以适用于这款CPU，但是由于具体实现的不同，Latency，Throughput 和 Functional Unit 的具体数值不同，具体可以参考这份手册，访问有困难可以下载本站托管版本。手册的第二章讲解了 Functional Unit 及其流水线，第三章列出了各个指令可用的 Functional Unit，以及 Latency, Throughput 数据。

Tips: - 第三章开头说明了手册中 Latency 和 Throughtput 的意义。 - 查阅手册时可以使用 Ctrl+F (Mac上是 Command+F) 快捷键查找你需要的指令。

本实验编译 C 程序时都开启-O2优化。

知识回顾¶

CPE¶

CPE

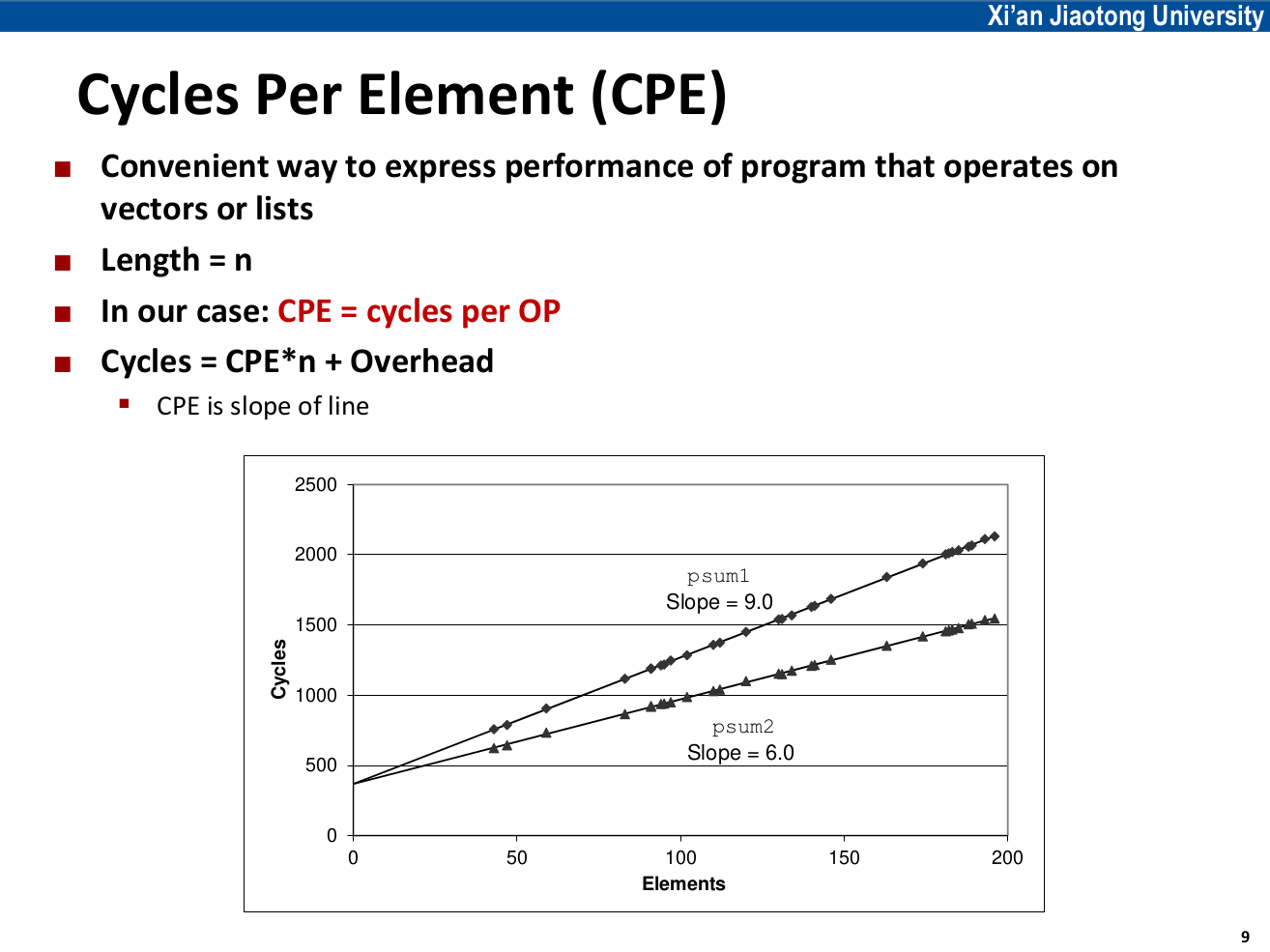
课本上提出了CPE(Cycle Per Element)的概念，用于方便地描述操作数组的函数的性能。如果一个函数对数组中的每个元素进行同种重复计算，那么可以测量每个“被计算的元素”平均花费的Cycle数，即CPE，数组长度n就是元素个数。

我们对不同的n分别测量整个函数花费的Cycle数，再以n为自变量，Cycle数为因变量进行最小二乘拟合，理想情况下会得到一条直线。这条直线的斜率就是CPE，直线的截距就是循环之外部分的开销，与n无关。

Latency bound¶

Latency

当我们连续多次进行同种运算时，如果这些运算之间存在数据依赖，那么这个依赖会成为限制程序性能的下界之一。观察下面这个计算前缀积的程序：

double product(double a[], long n)
{
    long i;
    double x = 1.0;
    for (i = 0; i < n; ++i) {
        x *= a[i];
    }
    return x;
}

变量 acc 的每次更新都需要等待上一轮循环的乘法运算完成之后才能进行。由于这个数据依赖的存在，CPE 的下界就提高到了一次浮点乘法的 Latency。

Throughput bound¶

假如我们消除了数据依赖，CPU 可以填满所有可用 Functional Unit 的流水线，那么CPE的下界在哪里呢？以浮点乘法举例，由于CPU有两个 Functional Unit，每个 Cycle 每个 Functional Unit 都可以发起一个新的乘法运算，那么每个 Cycle 可以处理两个Element，CPE 下界就是 1/2=0.5。

Functional Unit 的数量, Latency 以及 Cycles/Issue 值都是机器特定的。例如 ppt 上给出的 Haswell CPU 配置如下：

循环展开¶

要想突破 Latency bound 达到 Throughput bound，需要消除数据依赖。一个通用的方法就是循环展开。课上介绍了 2x1, 2x1a, 2x2, kxk 等多种展开方式。

`2x1` 展开¶

for (i = 0; i < limit; i+=2) {
    x = (x OP d[i]) OP d[i+1];
}

省去了分支预测开销，CPE 下界由数据依赖导致。

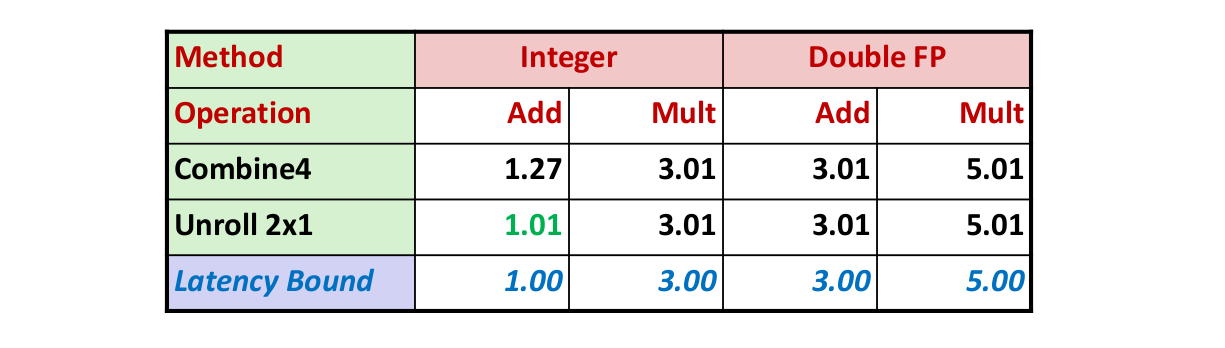
CPE-table

`2x1a` 展开¶

for (i = 0; i < limit; i+=2) {
    x = x OP (d[i] OP d[i+1]);
}

打破了数据依赖，x 的依赖路径变短了，从而突破了 Latency Bound。

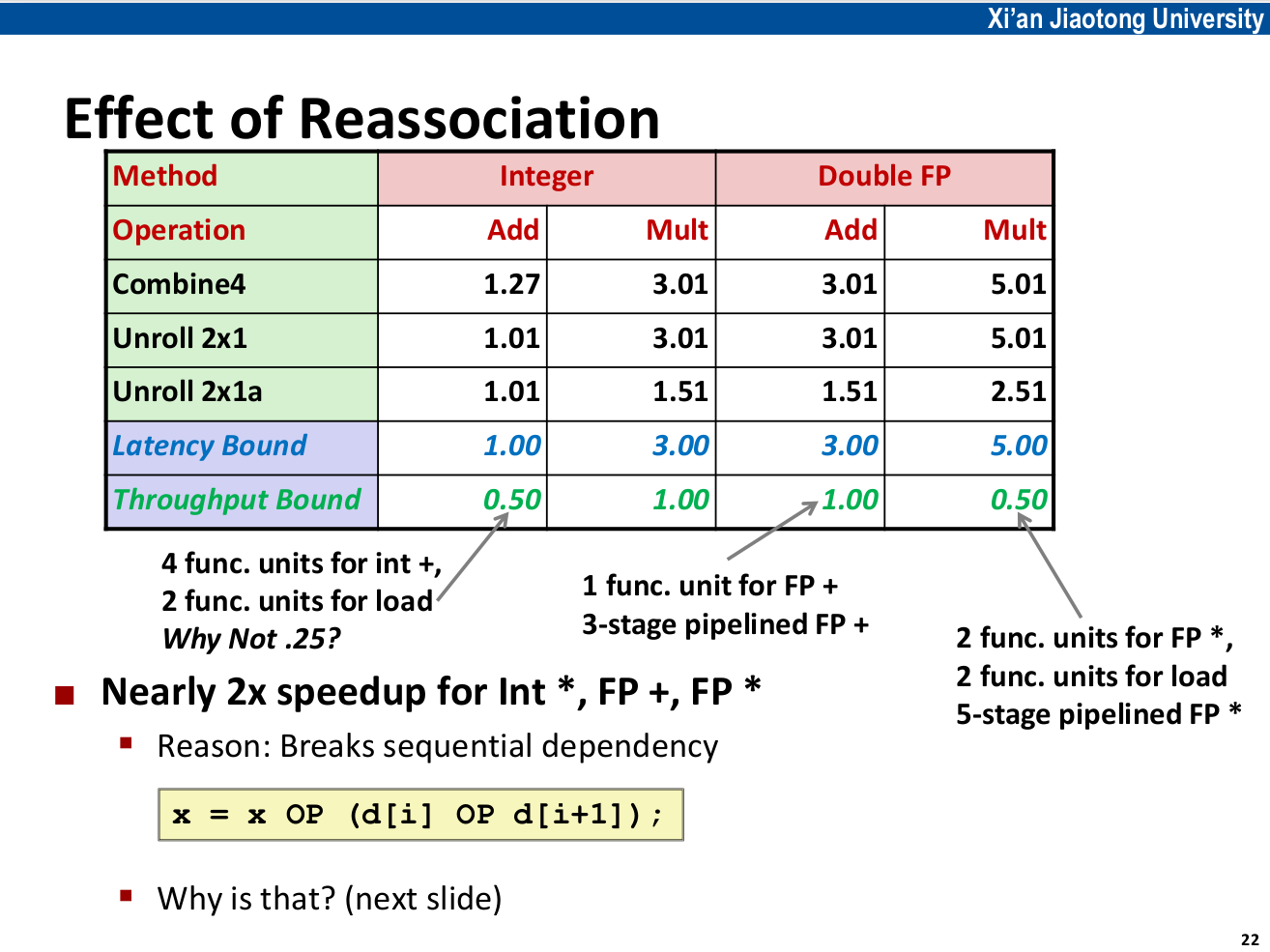
Dependency-2x1a 2x1a-cpe

`2x2` 展开¶

for (i = 0; i < limit; i+=2) {
    x0 = x0 OP d[i];
    x1 = x1 OP d[i+1];
}

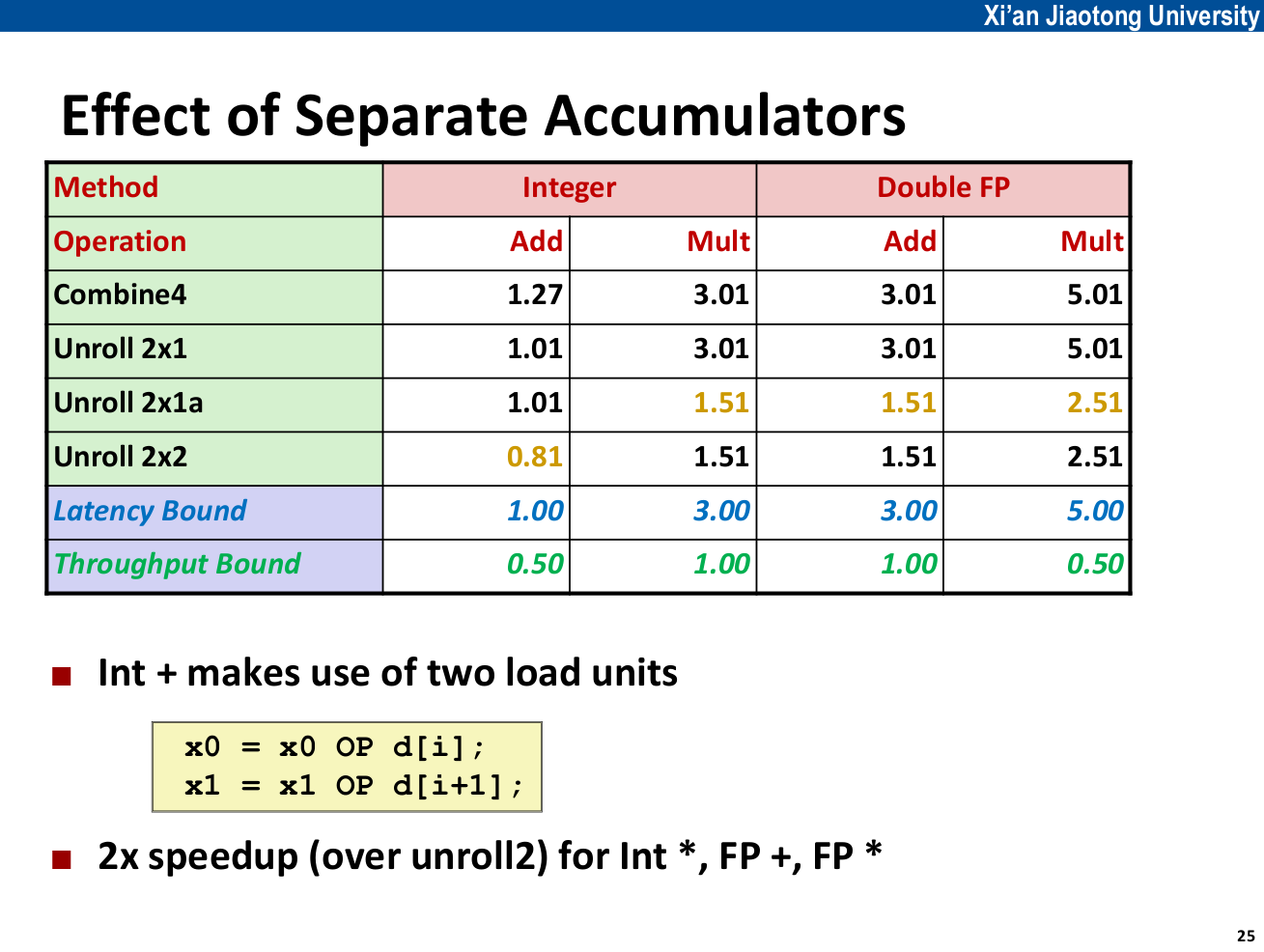
2x2-cpe

使用两个累积变量，从而两个操作可以分别在两条流水线上执行。

`kxk` 展开¶

总的来讲 kxk 展开在 k 足够高时，就可以消除循环间的数据依赖，从而CPE下界达到 Throughput Bound。

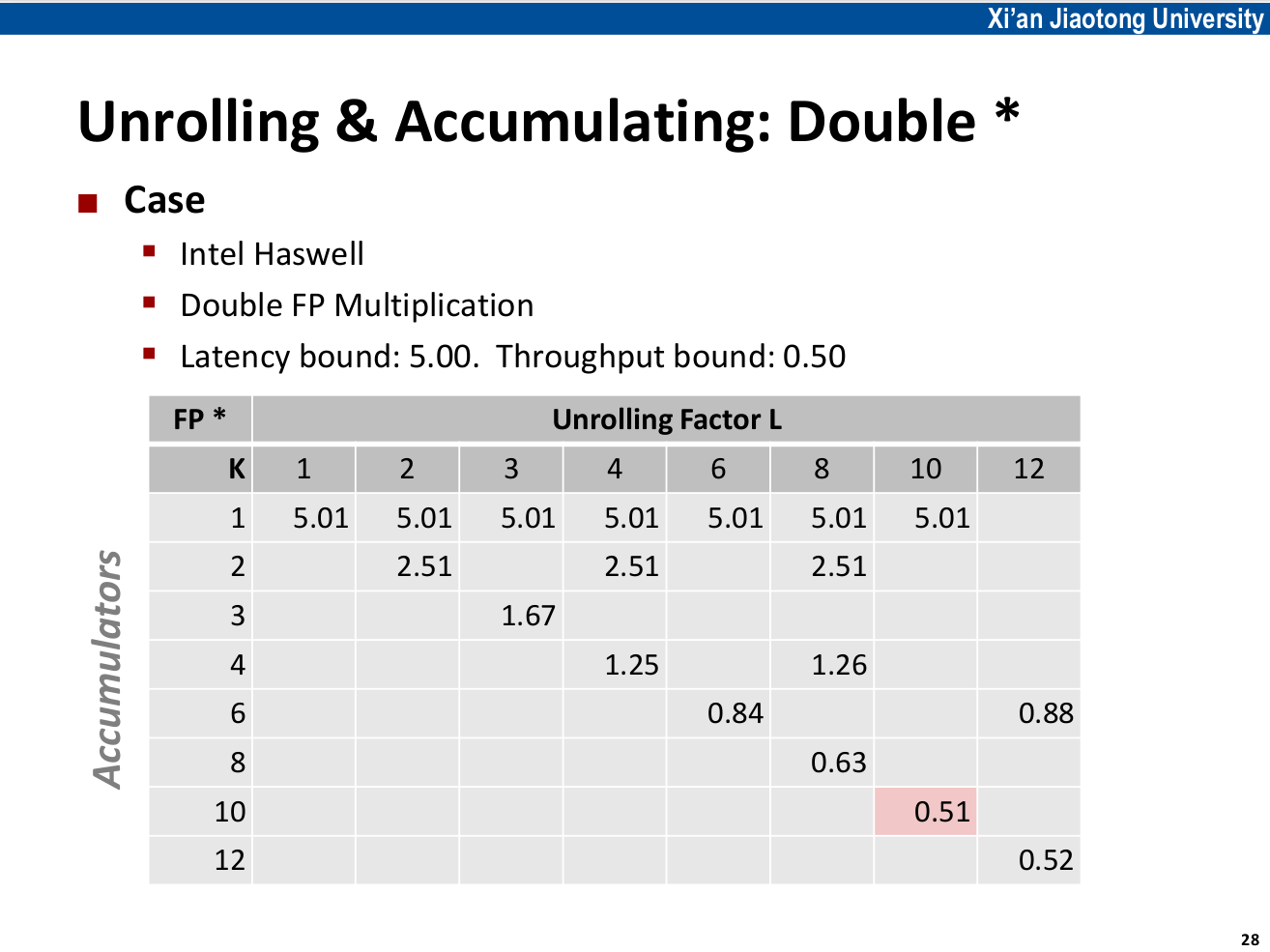
loop-unrolling

在 Haswell 机器上，以浮点数乘法为例作10x10展开，就可以达到0.5的Throughput Bound。

double product(double a[], long n)
{
    long i;
    double acc1 = 1.0;
    double acc2 = 1.0;
    double acc3 = 1.0;
    double acc4 = 1.0;
    double acc5 = 1.0;
    double acc6 = 1.0;
    double acc7 = 1.0;
    double acc8 = 1.0;
    double acc9 = 1.0;
    double acc10 = 1.0;
    for (i = 0; i + 9 < n; i += 10) {
        acc1 *= a[i];
        acc2 *= a[i + 1];
        acc3 *= a[i + 2];
        acc4 *= a[i + 3];
        acc5 *= a[i + 4];
        acc6 *= a[i + 5];
        acc7 *= a[i + 6];
        acc8 *= a[i + 7];
        acc9 *= a[i + 8];
        acc10 *= a[i + 9];
    }
    acc1 *= acc2;
    acc3 *= acc4;
    acc5 *= acc6;
    acc7 *= acc8;
    acc9 *= acc10;
    acc1 *= acc3;
    acc5 *= acc7;
    for (; i < n; ++i) {
        acc9 *= a[i];
    }
    return acc1 * acc5 * acc9;
}

每个循环体10次乘法，两个Functional Unit各负责5次。在下一个循环开始时，上一个循环的第一次乘法已经执行完成，于是新的乘法可以继续加入流水线。

然而，展开层数过高也不行，可能会因为寄存器数量不够而将临时变量存在栈上，内存的读写就成为了 CPE 的新的下界。

开始实验¶

打开家目录下的 optim 文件夹，应当有如下文件：

optim
├── main.c
├── Makefile
├── measure_time_std.o
├── poly.c
└── poly.h

这些文件可以随时从 /opt/optim_handout 中恢复。另外，我们鼓励大家使用 Git 管理源码，可以方便地看到自己的改动或回退到特定版本。

头文件 poly.h 中定义了：

宏 DEGREE：值为5000,表示多项式的最大度数（注意对于度数等于 DEGREE 的情况，a[0] 和 a[DEGREE] 都是多项式系数的一部分）
类型 poly_func_t：为函数指针类型起了别名，便于传参
poly()：秦九韶算法对多项式求值，已在 poly.c 中实现
poly_optim()：优化后的秦九韶算法对多项式求值，待实现
measure_time()：测量一个 poly_func_t 类型函数在给定数组长度下的运行时间，待实现
measure_time_std()：功能同 measure_time()，已在 measure_time_std.o 中实现，用于测试

poly.c 是本次试验你需要修改的文件。你需要实现 measure_time() 和 poly_optim() 两个函数，具体的要求下面会说明。

main.c 是测试框架，你不需要修改它，但你可以修改它来简化你的测试。

measure_time_std.o 中含有 measure_time_std() 的参考实现，测试脚本使用它来测量你的 poly_optim() 函数的性能。

Makefile 是构建测试程序的配置文件。输入如下指令：

linux$ make grade

会获得如下输出：

gcc main.c poly.c measure_time_std.o -o grader -O2
./grader

...

Total score: 0/100

现在你可以准备开始实验了。

Part A: 性能测量¶

下面的函数使用秦九韶算法实现了求多项式在某点处的值：

\[ \begin{align*} poly(x) &= a_0+a_1x+a_2x^2+...+a_nx^n \\ &= (((a_nx+a_{n-1})x+a_{n-2})x+...+a_1)x + a_0 \end{align*} \]

void poly(const double a[], double x, long degree, double *result) {
    long i;
    double r = a[degree];
    for (i = degree - 1; i >= 0; i--) {
        r = a[i] + r * x;
    }
    *result = r;
}

参数的意义为：

a: 多项式系数
x: 自变量
degree: 多项式的度数（注意a[degree]是多项式的最高次系数，没有off-by-1错误）

知识回顾部分中介绍了 CPE 的测量方法。本次实验中只需要同学们进行时间测量，曲线拟合操作由测试脚本进行。

Task:请你用C语言编写一个函数，测量这个函数的运行时间。

这个函数的原型如下：

void measure_time(poly_func_t poly, const double a[], double x, long degree, double *time);

各个参数的意义为：

poly: 多项式求值函数
a: 多项式系数
x: 自变量
degree: 多项式的度数
time: 输出测量得到的运行时间，单位为纳秒

注意到头文件中定义的 DEGREE 值了吗？本实验多项式度数不会超过 DEGREE (5000)。

为了避免系统中的其他负载等原因造成的明显离群点对曲线造成明显影响，测试代码会使用 RANSAC 算法自动去除离群点。如果你的测量结果过差，RANSAC 算法会返回 CPE=-1，这意味着你需要改进你的时间测量函数。

如果你经过自己的研究认为测试代码中的 RANSAC 算法实现对你的实验分数造成了不利的影响，你可以联系助教修复其中的问题。

注意事项¶

你可以使用最小二乘拟合的可视化工具（例如这个），看看你的实验结果在曲线上拟合得如何
查看编译器产生的汇编，看看和你的期望是否一致
这个函数的在鲲鹏920机器上的参考CPE是7.0，你应当能测到相当精确的结果

如何测量运行时间？¶

首先，5000是一个相对较小的值，所以测量时去除其他因素的影响十分重要。

Linux 系统下有若干函数用来测量运行时间：

clock()，一般为微秒粒度
gettimeofday()，微秒粒度
clock_gettime()，粒度可达纳秒（可以表示到纳秒，不代表真实精度为纳秒：例如真实精度可能是10ns，返回的纳秒数就一定是10的倍数）
- 这个函数还可以选择测量使用的时钟，具体的用法可以查看手册。同学们可以多多尝试，不同的时钟没有绝对的优劣。

请同学们查看这些函数的 man 手册，获得这些函数的用法。你可以根据你实验的结果选择测量函数，也可以参考这篇回答。

Hint：需要考虑时钟的精度，测量函数本身的消耗，以及时钟测量的时间的具体意义（真实时间？进程占用的CPU时间？）

可能遇到的坑¶

下面会介绍时间测量中可能会遇到的问题与解决手段。这些问题你不一定会全都遇到，这一节的目的在于遇到问题之后你可以来这里寻找可能的解释，以及你日后进行性能测试的时候可以参考。

OS调度¶

对测量值影响很大的一点是操作系统对进程的调度。每次调度都会产生context switch，这可能会导致TLB miss，cache miss等现象，如果出现频率很低、幅度很大的离群点，很有可能是操作系统调度的原因。实际运行过程中，这种离群点不多，测试框架会使用 RANSAC 算法去除这些离群点。

HOWTO: 你的代码不需要处理这一点：测试框架会处理。如果你感兴趣，可以看看测试框架中 RANSAC 算法的实现。

Cache miss¶

在执行你的时间测量函数前后，测试框架可能在执行其他任务，因此 L1 cache 中不一定存有数组的内容，可能会导致大规模的 cache miss。另外，由于每个L1 cache 都与核绑定，操作系统将进程调度到另一个核上也可能会导致 cache miss。

由于我们在测量CPE，我们不希望cache miss向结果中引入噪声，因此我们要在测试函数中手动预热cache。一个简单的方法是：在计时前先执行一遍待测函数，从而调入所需的cache。

实际上，测试脚本会在调用你的 measure_time 函数之前清空cache，以确保你有预热cache。

HOWTO: 在计时前先执行一遍待测函数，从而调入所需的cache。

其他¶

多次测量取平均，可以减少噪声的影响。

库函数可能会比你想象的重，例如 printf 甚至会涉及文件操作，可能会很大程度上污染你的 cache。

HOWTO: - 多次测量取平均，可以减少噪声的影响 - 谨慎调用库函数

Part B: 代码优化¶

Task: 运用课上学过的性能优化知识对这个函数进行优化，在 poly_optim() 函数中实现优化后的版本。

注意事项¶

我们能想到的最好的优化下，这个函数在鲲鹏920上的CPE可以达到1.0。如果你能想到更好的优化，你当然会在这个实验获得满分
实验过程中，你应当对你的实现的CPE有一个估计，然后看看实验结果是否符合你的预期
查看编译器产生的汇编，看看实际上发生了什么

评分方法¶

评分使用评测脚本。我们会在机器空载时进行测试，获得的分数应当只会比本地测试更高。所以如果你能在实验时稳定地达到 100 分，你的最终成绩应当是 100 分。如果最后对实验成绩有异议可以联系助教复核。

总共有4个测试点，每个测试点25分。

第一个测试点是使用你的 measure_time() 测量 poly() 函数的性能。参考 CPE 是 7，用你的测量结果拟合得到的 CPE 只要误差不超过 5%，即可通过该测试点。

我们会额外进行人工查验，所以不要尝试在 measure_time() 函数中 hard-code 运行时间。

第二个测试点是 poly_optim() 函数的正确性。如果多项式计算结果的相对误差不超过 \(10^{-10}\)（记 \(poly(x)=r_1\)，\(poly\_optim(x)=r_2\)，那么\(\frac{|r_1-r_2|}{r_1}\leq 10^{-10}\)），即可通过该测试点。

第三个测试点是 poly_optim() 函数的 CPE。使用 measure_time_std() 函数测量 poly_optim() 的 CPE，如果通过了第二个测试点，并且测得的 CPE 不超过 1.05 （即不超过参考 CPE 的 5%），即可通过该测试点。如果 CPE < 1，当然也会通过这个测试点。

第四个测试点是使用你的 measure_time() 函数测量 poly_optim() 函数的 CPE。如果你的测量结果与参考测量函数的测量结果相对误差不超过 5%（记参考测量函数测得 \(cpe_1\)，你的测量函数测得 \(cpe_2\)，那么 \(\frac{|cpe_1-cpe_2|}{cpe_1}\leq0.05\)），即可通过该测试点。

代码提交¶

在通过所有测试点后，在 /home/<username>/optim/ 目录中执行 make handin，就会在同一目录中得到一个名为 <username>-lab5-handin.zip 的压缩包。

压缩包中只有 poly.c 文件。这意味着你对其他任何文件的修改都不会在测试中被用到，所以请务必确认你在其他文件未修改时 make grade 仍然能够通过。再一次地，所有文件都可以从 /opt/optim-handout 中恢复，并且我们鼓励你使用 Git 管理源码，可以方便地看到自己的改动或回退到特定版本。

最终你只需要在在线学习平台上的作业模块中提交上述压缩包。

迟交¶

在超过原定的截止时间后，我们仍然接受同学的提交。此时，在lab中能获得的最高分数将随着迟交天数的增加而减少，具体服从以下给分策略：

超时7天（含7天）以内时，每天扣除3%的分数
超时7~14天（含14天）时，每天扣除4%的分数
超时14天以上时，每天扣除7%的分数，直至扣完

以上策略中超时不足一天的，均按一天计，自ddl时间开始计算。届时在线学习平台将开放迟交通道。

评分样例：如某同学小H在lab中取得95分，但晚交3天，那么他的最终分数就为95*(1-3*3%)=86.45分。同样的分数在晚交8天时，最终分数则为95*(1-7*3%-1*4%)=71.25分。

写在最后¶

我们将CPE的参考值告诉了同学们，是希望同学们实验时目标更加明确。虽然没有计分，但是分析编译器生成的汇编，思考CPE为什么是这个值，性能瓶颈究竟在哪条指令上，也是这个实验很重要的一部分。

这里再布置两道思考题，同学们可以通过解答这两个问题来检验自己对实验的理解。

如果使用 poly() 同时计算多项式在两个 \(x\) 处的值，运行时间如何？14个值呢？需要计算 14 个值时，使用一次 poly() 同时计算快，还是调用14次 poly_optim() 快？
为什么优化后的函数 CPE 是 1 而不是 0.5，性能瓶颈在哪里？（如果你确实得到了低于 1 的CPE，可以联系助教探讨你的做法）

这个实验在真实系统中测量性能，有操作系统这座大山隔在你和CPU之间。所以，如果你碰到疑难的问题，并且经过思考和调查仍然没有得到答案，欢迎联系助教，我们共同学习、共同解决。

XJTU-ICS Lab 5: Optimization Lab¶

实验简介¶

实验环境准备¶

注意事项¶

知识回顾¶

CPE¶

Latency bound¶

Throughput bound¶

循环展开¶

2x1 展开¶

2x1a 展开¶

2x2 展开¶

kxk 展开¶

开始实验¶

Part A: 性能测量¶

注意事项¶

如何测量运行时间？¶

可能遇到的坑¶

OS调度¶

Cache miss¶

其他¶

Part B: 代码优化¶

注意事项¶

评分方法¶

代码提交¶

迟交¶

写在最后¶

`2x1` 展开¶

`2x1a` 展开¶

`2x2` 展开¶

`kxk` 展开¶